0%

LeetCode 1457. Pseudo-Palindromic Paths in a Binary Tree

Posted on Edited on In

题目

原题在此
Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.
Return the number of pseudo-palindromic paths going from the root node to leaf nodes.
Example 1:

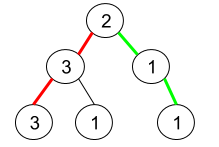
Input: root = [2,3,1,3,1,null,1]
Output: 2
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).
Example 2:

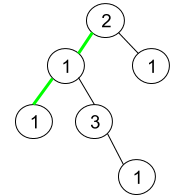
Input: root = [2,1,1,1,3,null,null,null,null,null,1]
Output: 1
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).
Example 3:

Input: root = [9]
Output: 1

Constraints:
The given binary tree will have between 1 and 10^5 nodes.
Node values are digits from 1 to 9.

分析

  1. 要判断从root到leaf的所有数字是否能组合成一个回文串,只需要判断每个数字出现的是奇数次还是偶数次.其中,如果有超过1个的奇数次则不可能组成回文串.
  2. 一开始会想用map<int, int>来储存每个数字出现了奇数次还是偶数次.仔细思考发现,key的情况只有0-9的10种情况,而value我们只关心奇偶性.所以可以用一个integer来代替map,对第n位做异或操作来改变奇偶性.
  3. 这时,计算integer中1出现的次数可以用汉明重量.

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res = 0;    
    int pseudoPalindromicPaths (TreeNode* root) {
        dfs(root, 0);
        return res;
    }

private:
    void dfs(TreeNode* root, int odd) {
        if(!root) return;
        odd ^= (1 << root->val);
        if(!root -> left && !root -> right) {
            if(hammingWeight(odd) < 2) res++;
            return;
        }
        dfs(root->left, odd);
        dfs(root->right, odd);
    }

    int hammingWeight(uint32_t i) {
        i = (i  & 0x55555555) + ((i >> 1) & 0x55555555);
        i = (i & 0x33333333) + ((i >> 2) & 0x33333333);
        i = (i + (i >> 4)) & 0x0f0f0f0f;
        i = (i + (i >> 8)) & 0x00ff00ff;
        i = i + (i >>16) & 0x0000ffff;
        return (int)i;
    }
};