0%

LeetCode 84. Largest Rectangle in Histogram

Posted on Edited on In

题目

题目链接
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.
Example:

Input: [2,1,5,6,2,3]
Output: 10

分析

暴力搜索

依次取区间arr(i..j),用min(arr(i..j)) * j - i可以遍历所有可能的长方形,从中选取最大的即可.此时时间复杂度为$O(N^2)$.
观察暴力解法发现:

  1. 最大面积的长方形长度必然和数组中的某个元素的值相等.即在数组中只有arr.length个候选最大长方形.此时我们要设法确定每个元素高度的长方形的宽度.
  2. 暴力搜索的过程没有做任何记录,每次搜索对下一次没有任何帮助,可以设法记录有效信息简化搜索过程.即空间换时间.
  3. 输入数组元素均为非负整数,在数组两侧各添加一个0不改变最终结果(哨兵,Sentinel).如此可省略处理edge case的部分,简化代码.

算法改进

在当前元素严格小于上一个元素时,便决定了此前某些元素的宽度无法再拓展了.此时以当前下标为右界,上一个元素的下标为左界,便可确定以此元素为高的矩形的宽度.
我们可以用栈存下标.就拿例题来说,左侧哨兵下标i=-1,循环前先入栈.

  1. i = 0,a[i] = 2 还有继续向右拓宽的可能,下标入栈.
  2. i = 1,a[i] = 1 此时:
    1. 栈尾元素a[s.back()],即下标为0的元素2大于当前元素.高度为2的长方形无法再拓宽,退栈处理.宽度为当前下标1减去退栈后的栈尾元素下标此时为哨兵-1再减去1,即width = i - s.back() - 1; area = width * height;.
    2. 再次检查栈尾,发现哨兵高度为0还有拓宽可能,不做处理(这样可能更好理解一些,实际情况是栈内只剩下哨兵,不做处理.再第四步还有一次演示).
    3. 当前下标元素也有拓宽可能,下标入栈.
  3. i = 2,a[i] = 5;i = 3,a[i] = 6 还有继续向右拓宽的可能,入栈.
  4. i = 4,a[i] = 2 与第二步做相似处理,先后确定了以6和以5为高度的长方形的面积.在6,5分别退栈后访问到a[1],发现当前下标元素不小于a[1].即栈内所有元素均还有拓宽可能,故不作处理.当前下标也入栈.
  5. i = 5,a[i] = 3 还有继续向右拓宽的可能,入栈. 再次强调哨兵
  6. i = 6,a[i] = 0 元素访问完毕,下标来到哨兵,此时栈内除了另一个哨兵外元素全部大于哨兵.对栈内元素依次退栈计算面积,直到栈内只剩下哨兵为止.
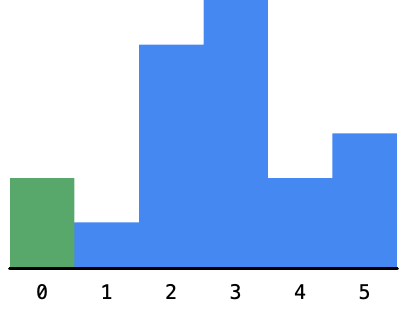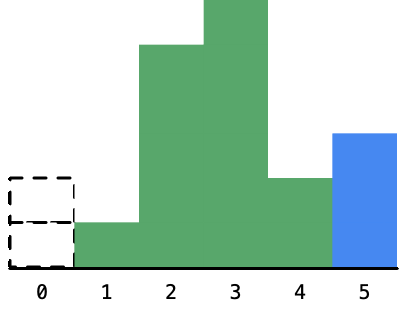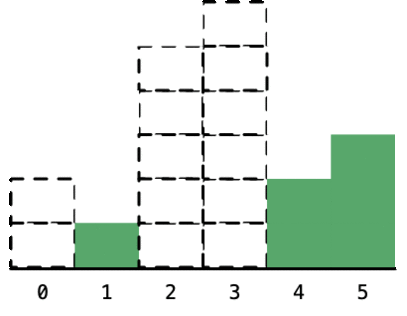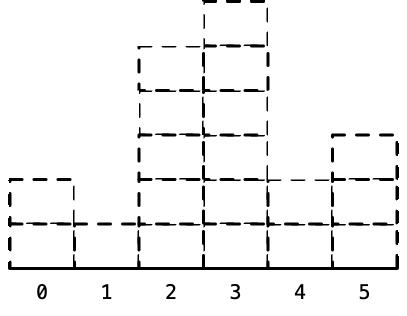
  • 绿色:宽度还有可能变长,入栈. 红色:宽度无法拓展,出栈计算面积. 虚线:以此元素为高度的长方形面积已确定. (要想象首尾各有一个0)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int res = 0;
        vector<int> stack;
        heights.push_back(0);
        stack.push_back(-1);
        for(int i = 0; i < heights.size(); ++i) {
            while(stack.size() > 1 && heights[stack.back()] >= heights[i]) {
                int h = heights[stack.back()];
                stack.pop_back();
                res = max(res, h * (i - stack.back() - 1));
            }
            stack.push_back(i);
        }
        return res;
    }
};

后续

  1. 在有连续个值相同的元素时,中间会有多次错误计算,但并不影响连续元素中最后一次退栈的计算成为最大值.
  2. JAVA-为什么用Deque去实现Stack?