题目

原题在此
You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route’s effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

Example 1: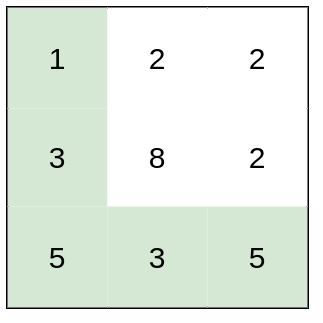

Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5]has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2: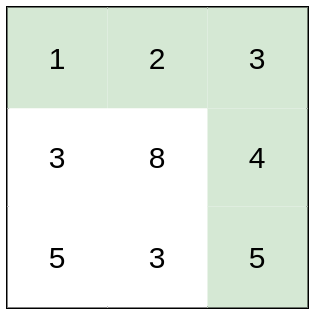

Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3: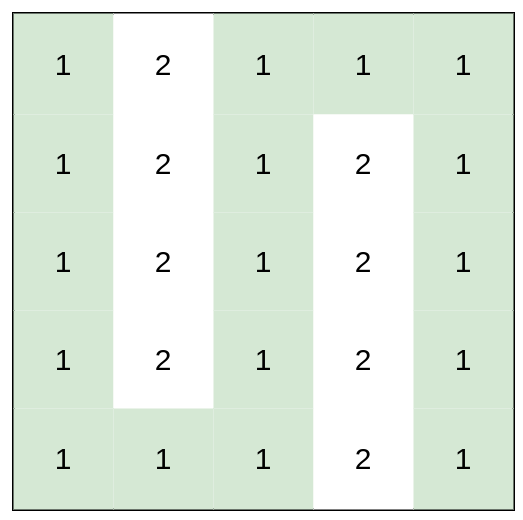

Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

Constraints:

rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 106

解析

以graph的视角来看的话, 相邻node间的距离是node.val差的绝对值. 此时题目转化为求起点到终点的路径中单次距离最短的路径.
求路径就会想到Dijkstra算法. 但是在普通Dijkstra算法顺次计算距离的过程会造成TLE, 可以使用优先队列维护一个{effort, x, y}的三元组, 在必要的时候再搜索路径.

代码

c++

class Solution {
public:
    int minimumEffortPath(vector<vector<int>>& m) {
        int row = m.size(), col = m[0].size();
        int dir[5] = {0, 1, 0, -1, 0};
        vector<vector<int>> efforts(row, vector<int>(col, INT_MAX));
        auto compare = [&](const array<int, 3> &p1, const array<int, 3> &p2) { return p1[0] >= p2[0]; };
        priority_queue<array<int, 3>, vector<array<int, 3>>, decltype(compare)> pq(compare);
        pq.push({0, 0, 0});
        efforts[0][0] = 0;
        
        while(!pq.empty()) {
            auto [e, r, c] = pq.top();
            pq.pop();
            if(r == row - 1 && c == col - 1) break;
            
            for(int i = 0; i < 4; i++) {
                int x = r + dir[i], y = c + dir[i + 1];
                if(x >= 0 && y >= 0 && x < row && y < col) {
                    int effort = max(e, abs(m[r][c] - m[x][y]));
                    if (effort < efforts[x][y]) {
                        efforts[x][y] = effort;
                        pq.push({effort, x, y});
                    }
                }
            }
        }
        return efforts[row - 1][col - 1];
    }
};