0%

1091. Shortest Path in Binary Matrix

Posted on Edited on In

题目

原题在此

In an N by N square grid, each cell is either empty (0) or blocked (1).

A clear path from top-left to bottom-right has length k if and only if it is composed of cells C_1, C_2, ..., C_k such that:

  • Adjacent cells C_i and C_{i+1} are connected 8-directionally (ie., they are different and share an edge or corner)
  • C_1 is at location (0, 0) (ie. has value grid[0][0])
  • C_k is at location (N-1, N-1) (ie. has value grid[N-1][N-1])
  • If C_i is located at (r, c), then grid[r][c] is empty (ie. grid[r][c] == 0).
    Return the length of the shortest such clear path from top-left to bottom-right. If such a path does not exist, return -1.

Example 1:
Input: [[0,1],[1,0]]
Output: 2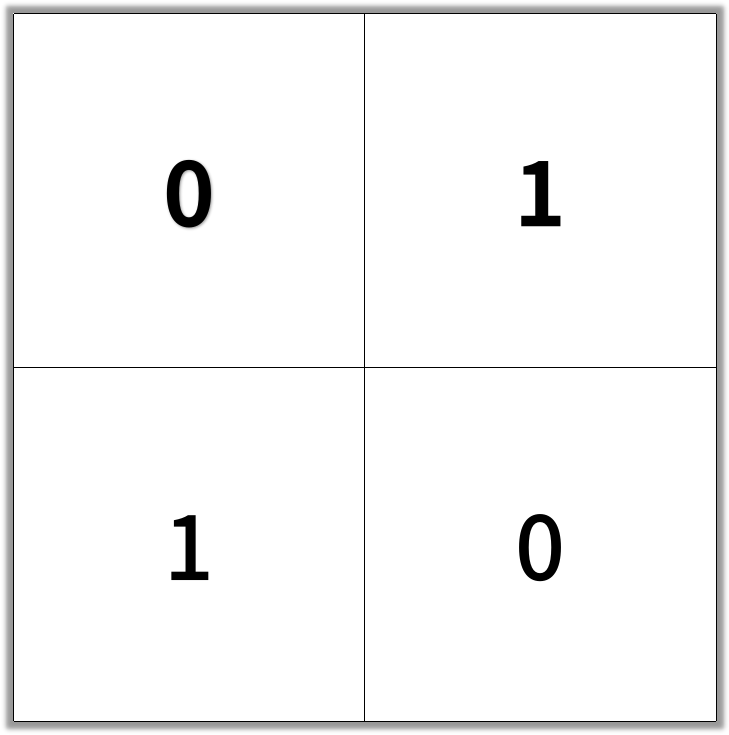

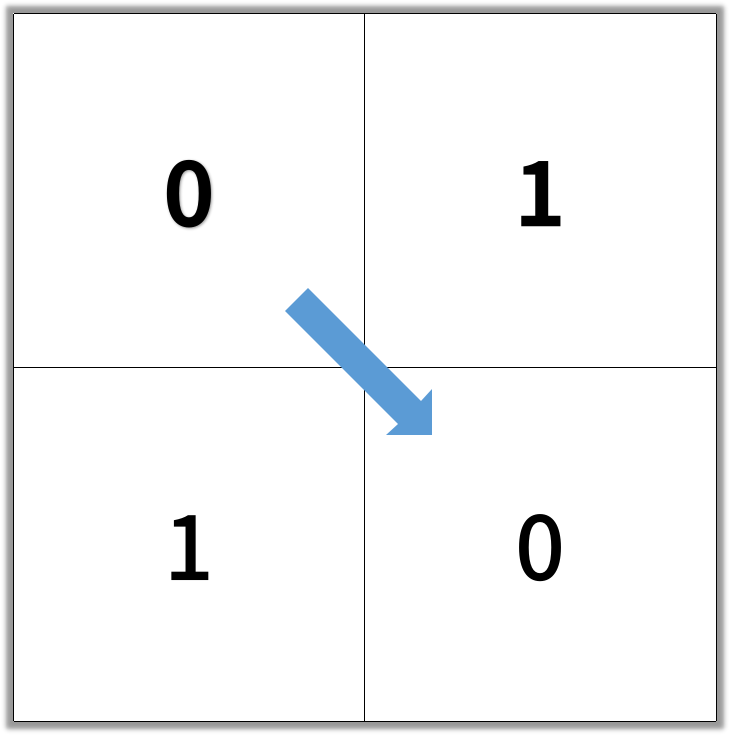
Example 2:
Input: [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

Note:

  • 1 <= grid.length == grid[0].length <= 100
  • grid[r][c] is 0 or 1

解析

典型的BFS算法, 用queue维护待搜索节点, 搜索过的节点要标注以避免死循环.

代码

c++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
        if(grid.empty() || grid[0][0]) return -1;
        queue<pair<int, int>> q;
        q.push({0,0});
        grid[0][0] = 1;
        int len = 1, n = grid.size();
        vector<int> dir{1,0,-1,0,1,1,-1,-1,1};
        while(!q.empty()) {
            int size = q.size();
            for (int i = 0; i < size; ++i) {
                auto [x, y] = q.front();
                q.pop();
                if(x == n - 1 && y == n - 1) return len;
                for(int j = 0; j < 8; ) {
                    int row = x + dir[j];
                    int col = y + dir[++j];
                    if(row >= 0 && row < n && col >= 0 && col < n && !grid[row][col]) {
                        q.push({row, col});
                        grid[row][col] = 1;
                    }
                }
            }
            len++;
        }
        return -1;
    }
};